前言
反馈现象存在于世界的各个角落,影响到我们生活的方方面面。不仅在物理学中,在其他自然科学领域甚至人文科学领域,都广泛存在着各 式各样的反馈现象。 我们日常生活中经常提到的恶性循环与良性循环,实质上就是不同的反馈现象。比如,有的同学出现了夜里睡眠不良的问题,就可能影响 学习效率。学习效率降低又会使同学延长夜里的学习时间,加重睡眠不良的问题。这实质上是一个正反馈,正是由于正反馈形成了这样一个恶性循环。 深入地了解反馈现象的各种性质,对我们学好物理学及相关科学技术,如电子学、计算机科学等很有帮助。同时,由于反馈现象产生的各种 特性也往往可以类推到其他学科。
一、杂技中的正负反馈
听上去,反馈现象距离我们生活很遥远,但其实存在于很多司空见惯的事物与现象当中。这里我们首先做个简单的实验,以获得反馈现象的 感性认识。
- 实验现象
找一些长短不一木棒,用食指托住一根木棒的下端,让木棒保持树直状态,不要翻到,如图所示。如果我们手指不动,木棒很快会翻倒。要 想保持木棒竖直,我们的手指必然下意识地随着木棒歪斜的方向作出调整。如果切换不同长度的木棒重复这个实验,就会发现比较长的木棒比较容易保持不倒。不同的人,可以支撑的最短木棒的长度可能会不同,而同一个人,经过一定练习,也有可能支撑原来支撑不了的短木棒。
2. 分析与讨论
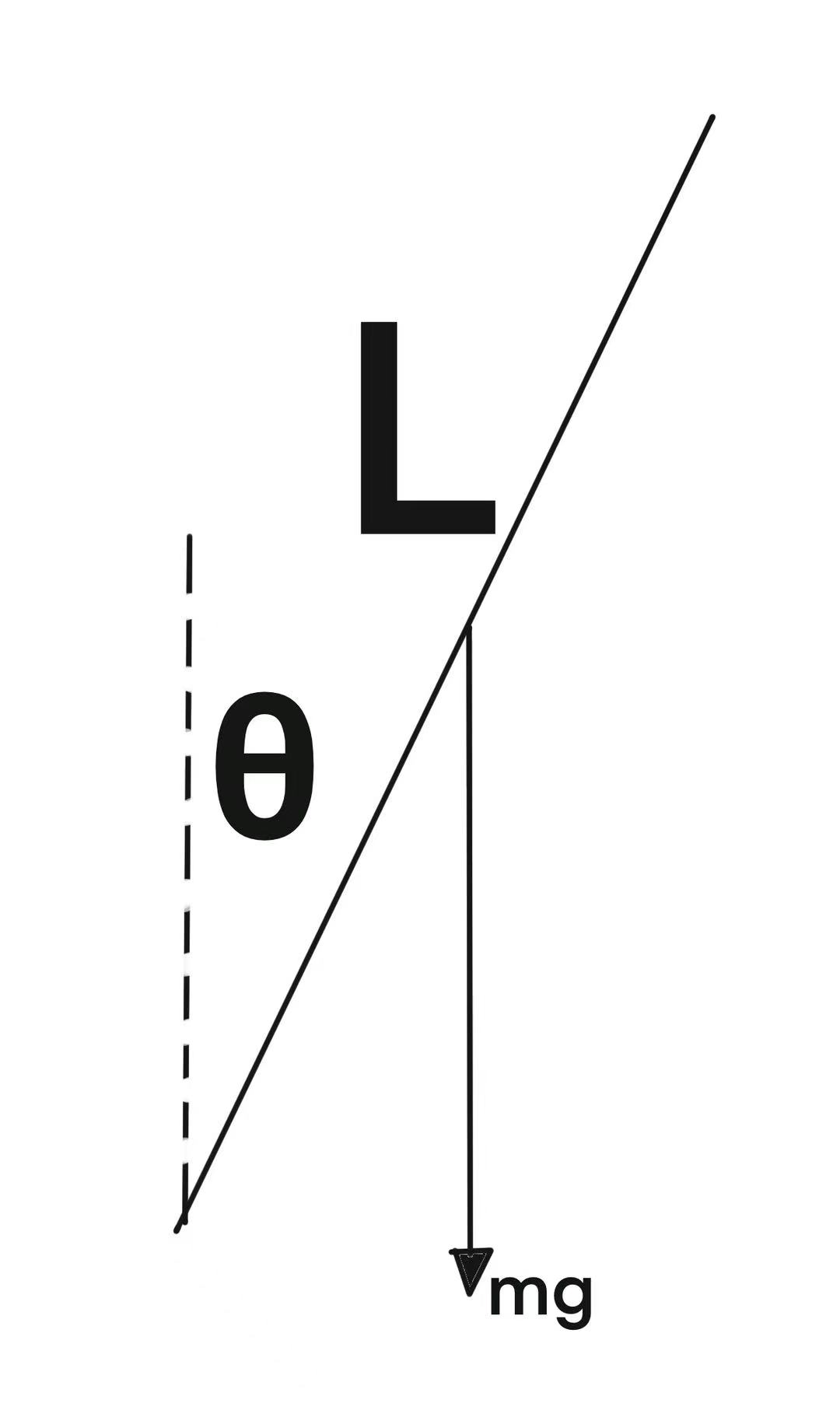
这个现象可以用正负反馈的概念来讨论,反馈通常是指某一个物理量的变化,通过一个系统,反过来又影响到这个物理量。如果系统的反馈 造成这个物理量的变化继续增加,则这种反馈叫正反馈,反之则是负反馈。 木棒倒下毫无疑问是一个正反馈。从图中可以看出,当木棒稍稍偏离正中位置一个角度θ时,木棒的重力作用线偏离支点,产生一个力矩。这个力矩使得木棒产生一个角加速度\(θ^{''}\),如下所示: \(Iθ^{''}=mg\frac{L}{2}\sinθ\) 式中,g是重力加速度;m、I、L分别是木棒的质量、转动惯量和长度。 \( a \times b = c ^ b \) \( 2^{\frac{n-1}{3}} \)
这个角加速度倾向于使木棒偏离正中位置的角度继续增加,而当偏离的角度进一步增加时,这个角加速度也进一步增大。当我们让木棒从支点上自由歪倒时,可以看到木棒一开始很慢的偏离正中位置,随后偏离的速度越来越快,因此这是一个正反馈的机制。而木棒围绕一端旋转时的转动惯量为 \(I=(1/3)mL^2\)。 于是,经过简化可以得到下式: \(θ^{''}=g\frac{3}{2L}\sinθ\) 不难看出,木棒歪倒过程中的角加速度与偏离正中位置的角度及木棒的长度有关,与木棒的质量无关。也就是说,无论重的或轻的木棒,它们从某个角度歪倒到另一个角度所需的时间是一样的(我们假定它们的初始状态都是静止的,或者初始的角速度是相同的)。 在这个实验中,我们的手指起到什么作用呢?事实上,眼睛、大脑和手指组成了另一个系统,这个系统提供了一个负反馈的机制。在支撑木棒时,我们用眼睛感知木棒与正中位置的偏差。根据这个偏差的方向与大小,我们的大脑向手指发出移动的指令。手指移动使得木棒的偏差减小,从而实现负反馈。当负反馈与正反馈机制同时存在时,负反馈作用必须比正反馈强,才能使总的反馈效应为负,使系统相关的参量处于一个中间值附近,而不是变化到极端值。对我们这个系统而言,就是保持木棒竖直。

对比长木棒和短木棒,它们歪倒过程中的角加速度是不同的,在倾斜角相同的情况下,长木棒的角加速度比较小,也就是说,长木棒的正反馈性质比较弱。我们再比较它们的负反馈性质。对于比较长的木棒,我们可以在它偏离正中位置的角度很小的时候就及时察觉到,使得大脑及时作出判断,发出移动手指的指令,这样就使得负反馈的作用比较有效,可以超过正反馈的作用。长木棒的正反馈效应比较弱,而负反馈效应比较强,这就是长木棒比较容易保持竖直的原因。 我看到杂技演员走钢丝时,手会持一根很长的平衡棒,目的也是通过减小演员与平衡棒歪倒的角加速度,使演员有更长的时间做出调节反应,以保持在钢丝上的平衡。 这样一个保持木棒竖直的负反馈系统,也可以用现代技术来实现。比如,可以用摄像头来测定木棒的偏差角度,通过计算机计算,来驱动一个xy二维运动平台以纠正木棒偏差,如图所示。这样一个系统可以用来验证角度传感器与处理软件及计算机的运算能力,同时刻意用来测试运动平台的机械反应速度与精度。
上图为一个二阶倒立摆实验系统。关于倒立摆的实验早在上世纪九十年代北京航空航天大学自动化系就已经成功的实现了,如今这样一个负反馈系统甚至可以用四轴飞行器来实现,以此验证更多的新技术和新产品。
有什么问题呢?-没问题
文章摘自 吴进远 著《触物及理》 略有改动