线性或非线性通常是指在一个系统中,输出物理量随着输入物理量变化的函数关系。比如,对一个扬声器输入一个电信号,其输出声压与输入的电信号相关。在真实系统中,这种函数关系的复杂性有两个方面:首先,输出量不仅与输入量本身有关,还可能与输入量的变化速率有关;其次,输出量的增减与输入量的增减可能不一定成比例,也就是说,系统可能不一定是线性的。
一、大振幅与非线性效应
首先介绍一下系统的非线性是怎么回事。
- 非线性的概念
对于一个输入输出量分别为x和y的系统,它们之间可能存在如下的函数关系:\( f\left(x,x^{'},x^{''},\,…\right) \) 其中,\(x,x^{'},x^{''}\)为输入量及其一阶与二阶时间变化率(如果x是物体的位移,则它的一阶与二阶时间变化率分别是速度与加速度)。 很多系统的函数关系式可以进一步简化为 \(y=ax+a_1x^{'}+a_2x^{''}+…\) 这种系统叫做线性系统,在线性系统的函数关系式中只有x、\(x^{'}\)、\(x^{''}\)的一次项存在,而没有\(x^2、x^3、x^{'2}、x^{''2}、\)等高次项存在。这里注意,不要把高次项与高阶变化率两个不同的概念混淆。线性系统是指函数中只存在一次项,而没有高次项。最常见的一个例子是弹簧,弹簧的伸长量或缩短量在一定的范围内与外力的大小成正比,符合胡克定律:\(f=-kx\)。如果 把这个关系式画出图形,以x为横坐标,\(f\)为纵坐标。这个函数就是一条直线。线性这个名称就是这么来的。当一个系统中的物理量之间存在线性关系时,这个系统的运动或变化行为相对比较简单,也比较容易研究。事实上,线性系统的理论也是人们在数学上研究得比较透彻的一个重要分支。因此,在很多学科中,人们往往把各种复杂的系统首先近似地看成线性的,而由于这种线性近似,许多不同学科的系统经常会呈现很多类似性质。然而严格地说,实际系统几乎没有线性的。比如弹簧,当外力大到一定程度时,其形变就可能不再与外力成正比。又比如我们学过的单摆,它的恢复力由和偏离中心的角度成正弦函数关系,\(f=mg\sinθ\),显然也是非线性的。
2. 振幅与非线性
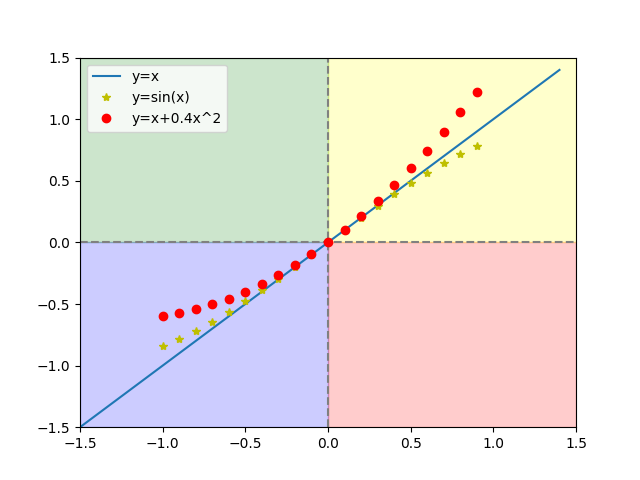
对于非线性系统,如果相关的物理量平衡位置很小,使用线性近似带来的误差也很小。我们可以从图看出这点。不难看出,对于一个非线性系统,当输入量接近于0时,其特性曲线与直线几乎重合。这告诉我们,在输入量的振幅不大时,一个真实系统尽管可能是线性的,仍然可以用对线性系统得到的结论来近似。而如果输入量的振幅增大,非线性效应就无法忽略,但很多情况下仍然看成是在线性基础上叠加一个小的修正:\(y=ax+{a_1}x^{'}+{a_2}x^{''}+bx^2+{b_1}x^{'2}+{b_2}x^{''2}+…\)
其中高次项只在振幅比较大的情况下起显著作用。
二、倍频现象
非线性系统与线性系统的一个重要区别是正弦信号通过它们时输出信号的不同。当一个正弦信号通过线性系统时,信号的振幅与相位都可以不同,但输出信号仍然是一个正弦信号,其频率与输入信号频率一样。而当一个正弦信号通过非线性系统时,输出信号中可能含有输入信号频率的两倍、三倍乃至更高倍数的频率成分。这种现象叫做倍频现象。我们通过一个简单的实验来观察倍频现象。在这个实验中,我们会用到两部手机,分别下载两个不同的APP。
- 下载安装APP和初步调试
在智能手机APP商店中,输入关键词“信号发生器”或“signal generator”,就可以找到很多可以让手机发出正弦波的APP,从中挑选能产生多个正弦波的。笔者用的是Multi Wave,在安卓系统可以使用一款名叫Function Generator的APP。在第一部手机上安装这个正弦波发生器的APP,在第二部手机上下载安装一个SpectrumView 的APP。
2. 倍频信号的观察
启动第一部手机的正弦波发声器,可以从手机的扬声器中听到一个单一频率的声音,调整输出声音的频率至2000~2500Hz。启动第二部手机的频谱仪,这时,从频谱仪上可以看到对应第一部手机所发出声音的频谱线。将两部手机从间隔30厘米左右的距离逐渐推近靠拢,直至第一部手机的扬声器正对第二部手机的话筒,两者间距小于1厘米,如图。在两部手机逐渐接近的过程中,第二部手机的话筒接收到的声音振幅逐渐增加。手机的话筒与内部的放大器系统多少存在一些非线性失真,在信号很强的情况下,这种失真就会出现比较显著的倍频效应。 这个实验中,我们可以得到一个频谱图。在这个图中,横坐标是时间,单位是秒;总坐标是频率,单位是赫兹。这个频谱图显示的是在某一时间,手机话筒测得的声波所包含的频率成分。图中的颜色表示这些频率成分的强度。 我们做这个实验时,第一部手机发出正弦波的频率为2200Hz,从图中可以看出,当两部手机距离比较远时,频谱图中只能看到2200Hz的频率成分,我们通常称这个原始的频率为基频。在信号不很强的情况下,几乎看不到二倍或三倍频的成分。当两部手机贴近后,可以看到4400Hz和6600Hz的频率成分逐渐增强,出现了显著的二倍三倍频效应。 3. 倍频原理
现在解释一下为什么存在非线性失真的系统会生成倍频信号。为了简化数学运算,我们忽略前面提及的信号变化率带来的影响,这样可以得到\(y=ax+bx^2\)当输入信号为正弦波时,\(x={x_0}\sin{\omega t}\),其中\({x_0}\)为输入信号振幅,\(\omega\)为正弦波的频率。上式的第一项即线性的贡献仍然是一个正弦信号,频率为原来的基频。而二次项的贡献可以写成
\(bx^2=b\left({x_0}\sin{\omega t}\right)^2=b{x_0}^2\left(1-\cos{2\omega t}\right)\)
由此可见,由于二次项的存在,系统生成了基频信号的二倍频成分。我们还可以看出,二次项的贡献与\({x_0}^2\)成正比,这表示只有在输入信号足够强的时候,二倍频的现象才会比较显著。
那么,途中三倍频成分又是怎样产生的呢?比较可能的一个机制是系统中存在三次项的非线性失真。通过类似上式的推导,很容易证明。当然真实系统中情况会更复杂。

三、单摆振幅与周期的关系
单摆在摆动幅度很小的时候,其运动可以看成简谐振动,振动的周期近似与振幅无关。不过,当振幅比较大的时候,其运动不再是简谐振动,振动的周期也会随着振幅的增加而变长。
- 原理简介
单摆的受力情况如图所示。单摆的恢复力是非线性的,由图可以得出恢复力f为 :
\(f=mg\sinθ\)
其中,mg为单摆锤所受到的重力,θ为摆的偏转角。将正弦函数展开:\(\sinθ\cong θ-\frac{θ^3}{3} \)

由此可见,恢复力中除了线性项(第一项)外,还存在非线性的高次项。非线性项在振幅很小的时候可以忽略,但是在振幅比较大的情况下,则不能忽略不计。这里,三次方的非线性项起到减小恢复力的作用,使得单摆回复原位的加速度变小,于是单摆的振荡周期在振幅比较大的情况下会略微变长一些。
2. 实验及数据分析
这里介绍一个简单的实验,以此获得对单摆振幅与周期的关系的直观理解。我们的实验装置是一个由细线和小重摆组成的单摆,如图
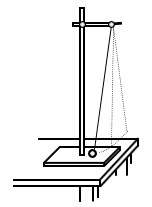
实验中用的单摆摆长大约90厘米,这个长度是根据悬挂点的高度决定的,我们希望单摆摆动时,可以尽量靠近地面掠过。我们在地面上贴一块黑胶带作为标记。
单摆的摆动周期在振幅为\(θ_0\)时可以通过下式计算:
\[T\cong2\pi\sqrt{\frac{L}{g}}\left(1+\frac{1}{16}{θ_0}^2+\frac{11}{3072}{θ_0}^4+…\right)\tag{3} \]
这个公式的具体推导过程比较复杂,感兴趣的读者可以查阅有关文献。当摆动振幅比较小的时候,高次项可以忽略,90厘米长的单摆摆动周长大约为1.9秒。为了验证这个结果,我们让单摆以大约5度的振幅摆动,并拍摄录像。单摆从左向右通过标记的情形如图。
我们把实验录像用计算机播放,通常数字照相机或手机拍摄的录像画面速度为30帧/秒,因此只要数出单摆摆动中两次通过同一位置之间的画面帧数,就可以计算出单摆周期。为了更加准确地确定单摆通过瞬间,我们选择从左到右,即将接触地面标记的位置作为计时的起点与终点。在这个状态下摆锤速度比较快,有利于通过比较相邻的两帧画面确认摆的位置。 用计算机软件启动录像后,将播放暂停,然后按动箭头键,选择作为起点的画幅。随后继续按键,以此数出单摆振荡一个周期所需要的画幅。为了提高精度,可以连续数若干个摆动周期,在笔者做的这个实验中,单摆在两个周期中共经过了114个画幅。由此计算出,这个单摆的振荡周期为 \(\left(114/2\right)/30=1.90\)秒 让单摆以比较大的振幅摆动,笔者在做实验时,摆的初始角度大约为45度,启动相机拍摄录像,然后重复前面的分析过程,这时单摆通过地面标记的速度比较快,因而影像比较模糊,如图,需仔细观察。实验中我们数了两个周期,单摆摆过这两个周期经过了119个画幅。由此算出,这个单摆的振荡周期 \(\left(119/2\right)/30=1.98\)秒 通过这个实验我们看出,当单摆振幅达到45度左右时,单摆的周期增加约4%,我们可以看与式<3>是否相符。在\(45^\circ\)时,\(θ_0=0.785\)(弧度),于是<3>式中的4次方项目前尚不显著。 有兴趣的读者可以进一步提高摆动幅度,如达到90度,这时式<3>中,除了平方项,4次方项也必须计入了。我们可以算出,在\(90^\circ\)时,4次方项对摆动周期的贡献达到2%的量级,用我们这个简单的实验装置可以测量出来,将摆动振幅为5、45、90度情况下的计算分析与测量结果在表中列出,可以看出非线性性质随着摆动振幅的增加逐渐显著的趋势。
| \(θ_0=0.087\) | \(θ_0=0.785\) | \(θ_0=1.571\) | |
|---|---|---|---|
| L | 0.90米 | 0.90米 | 0.90米 |
| \(2\pi\sqrt{\frac{L}{g}}\) | 1.90秒 | 1.90秒 | 1.90秒 |
| \(\frac{1}{16}{θ_0}^2\) | 0.0005 | 0.0385 | 0.1542 |
| \(\frac{11}{3072}{θ_0}^4\) | 0.0000 | 0.0014 | 0.0218 |
| T(计算值) | 1.90 | 1.98 | 2.23 |
| 画幅数 | 114/2 | 119/2 | |
| T(测量值) | 1.90 | 1.98 |
为了进一步提高实验精度,可以拍摄慢动作录像,通常慢动作录像的拍摄速度是120帧/秒乃至240帧/秒,可以大大提高测时精度。拍摄时注意要让光线强一些,这样可以尽量降低摆锤通过地面标记时的模糊程度。
文章摘自 吴进远 著《触物及理-令人眼界大开的物理小实验》
5