何为PID算法
我们提到过用于控制恒温的PID算法,那么何谓PID呢? PID控制原理和特点: 工程实际中,应用最为广泛调节器控制规律为比例、积分、微分控制,简称PID控制,又称PID调节。PID控制器问世至今已有70年历史,它以其结构简单、稳定性好、工作可靠、调整方便而成为工业控制主要技术之一。当被控制对象结构和参数不能完全掌握,或达不到精确数学模型时,控制理论其他技术难以采用时,系统控制器结构和参数必须依靠经验和现场调试来确定,这时应用PID控制技术最为方便。即当我们不完全了解一个系统和被控对象,或不能有效测量手段来获得系统参数,适合用PID控制技术。PID控制,实际中也有PI和PD控制。PID控制器就是系统误差利用比例、积分、微分计算出控制量进行控制。
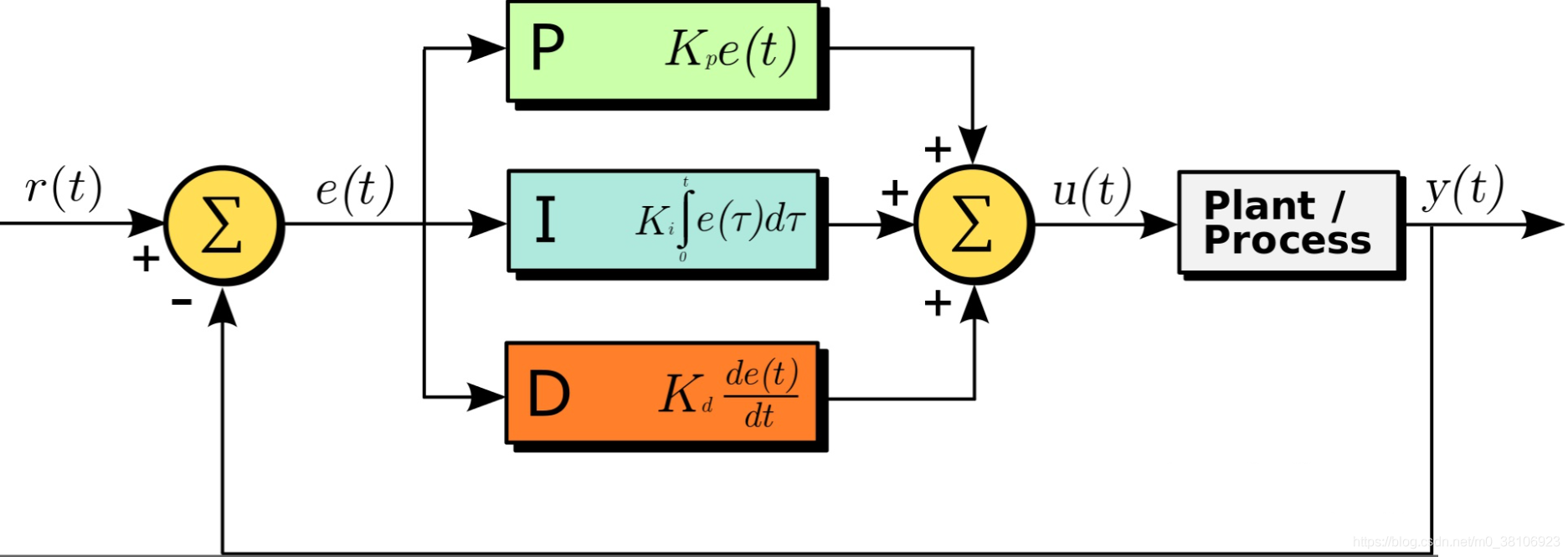
图中,\(r(t)\)是给定值\(\gamma(t)\)是实际输出,给定与实际输出值构成控制偏差\(\epsilon(t)\),\(\epsilon(t)=r(t)-\gamma(t)\)
\[\mu(t) = Kp[\epsilon(t)+\frac1{T_i} \int_0^t \epsilon(t) dt + Td \frac{d\epsilon(t)}{dt}]\] 其中: Kp ——控制器的比例系数 T i——控制器的积分时间,也称积分系数 Td——控制器的微分时间,也称微分系数
1. 比例部分
比例部分的数学式表示是:\(Kp\times\epsilon(t)\)
在模拟PID控制器中,比例环节的作用是对偏差瞬间作出反应,偏差一旦产生控制器立即产生控制作用,使控制量向减少偏差的方向变化,控制作用的强弱取决于比例系数,比例系数越大,控制作用越强,则过度过程越快,控制过程的静态偏差也就越小;但是比例系数越大,也越容易产生振荡,破坏系统的稳定性。故而,比例系数选择必须恰当,才能过度时间少,静差小而又稳定的效果。
2. 积分部分
积分部分的数学表示是:\(\frac{Kp}{T_i} \int_0^t \epsilon(t)dt\)
从积分部分的数学表达式可以知道,只要存在偏差,则它的控制作用就不断增加;只有偏差\(\epsilon(t)=0\)时,它的积分才能是一个常数,控制作用才是一个不会增加的常数。可见,积分部分可以消除系统偏差。 积分环节的调节作用虽然会消除静态误差,但也会降低系统的响应速度,增加系统的超调量。积分常数越大,积分的积累作用越弱,这时系统在过渡时不会产生振荡;但是增大积分常数\(T_i\)会减慢静态误差的消除过程,消除偏差所需要的时间也就越长,但可以减少超调量,提高系统稳定性。当\(T_i\)较小时,则积分作用较强,这时系统过渡时间中有可能产生振荡,不过消除偏差所需的时间较短。所以必须根据实际控制的具体要求来确定\(T_i\)。
3. 微分部分
微分部分的数学式表示是:\(Kp \times Td \frac{d\epsilon(t)}{dt}\)
实际的控制系统除了希望消除静态误差外,还要求加快调节过程。在偏差出现的瞬间,或在偏差变化的瞬间,不仅要对偏差作出立即响应(比例环节的作用),而且要根据偏差变化趋势预先给出适当纠正。为了实现这一作用,可在PI控制器的基础上加入微分环节,形成PID控制器。 微分环节的作用使阻止偏差的变化。它是根据偏差的变化趋势(变化速度)进行控制。偏差变化的越快,微分控制器的输出越大,并能在偏差值变大之前进行修正。微分作用的引入,将有助于减小超调量,克服振荡,使系统趋于稳定,特别对高阶系统非常有利,它加速了系统的跟踪速度。但微分的作用对输入信号的噪声很敏感,对那些噪声较大的系统一般不用微分,或在微分起作用前先对输入信号进行滤波。 微分部分的作用由微分时间常数\(Td\)决定。\(Td\)越大时,则它抑制偏差变化的作用越强;$Td$越小时,则它反抗偏差\(\epsilon(t)\)变化的作用越弱。微分部分显然对系统稳定有很大作用。 适当地选择微分常数\(Td\),可以使微分作用达到最优。 由于计算机的出现,计算机进入控制领域。人们将模拟PID控制规律引入到计算机中来。对\[\mu(t)=Kp[\epsilon(t) + \frac1{T_i} \int_0^t \epsilon(t)dt + Td \frac{d\epsilon(t)}{dt}]\] 的PID控制规律进行适当变换,就可以用软件实现PID控制,即数字PID控制。 通过上面对PID的简要介绍,大家对PID已经有了一个简单的了解了,在 KEYBOT mini中,我们设置的温度为给定值\(r(t)\),实际检测得到的温度为\(\gamma(t)\)两者之间的差值即为控制偏差\(\epsilon(t)\),控制偏差输入到PID控制器中,可以得到一个返回值\(\mu(t)\),这个\(\mu(t)\)作用于加热器,控制加热程度,从而保证了温度恒定不变。